# 0. 序
上一篇**【[谈谈二进制(一)](http://www.dubingxuan.com/article/edit/6/)】**中,我们花了巨量的篇幅,从最基本的计数开始,认识了各种进制的原理,接着通过对我们最熟悉的十进制的分解组合,推演了其他进制和十进制之间的相互转换过程。
本篇将继续深入二进制,来探究一下二进制的四则运算过程,也就是加、减、乘、除,看看二进制和十进制在计算上又有多少差异。
# 1. 加法
## 1.1 整数
加法一般是四则运算中首先被提及的,它是计数这一基础行为的延申,从一个一个地累加,延申到一堆一堆地相加,使计数这一行为提升了一个维度。按照上一篇文章的推演逻辑,我们依然从十进制开始,首先探究一下十进制的加法。
我们取两个十进制数:`62`和`185`,我们用简单的口算就能算出来他们俩的和是`247`,但这个运算过程是怎么样的呢?我们仔细想一下刚才在计算时大脑的计算过程,然后来看看小时候初学加法时用到的竖式表达式:

从上式中我们可以看到,这个加法的整个过程其实分为了四步:
1. 个位相加,得到的结果没有进位,依然是个位;
2. 十位相加,`6 + 8 = 14`,进位了,因为是十位的相加结果,所以进到百位上,因此十位上结果是`4`,百位上是`1`;
3. 百位相加,这里百位只有`185`的`1`,`62`的百位是`0`,所以是`0 + 1 = 1`;
4. 最后,把上面三步得到的结果再进行相加,数字不存在的空白处都看作是`0`,最终得到了`247`这个结果。
总结上面十进制的加法过程,其实就是两个数字从低位开始相加,如果有进位,就将进的位数加到下一位的计算结果上,然后重复这个过程,直到两个数字的所有位数遍历完成。
在上一篇文章中我们提到过,不同进制之间的区别几乎仅仅是进位方式的区别,所以上面这套加法法则在十进制数上成立,那么在二进制上自然也是成立的。我们取两个二进制数字`101`和`1110`,把它们相加:
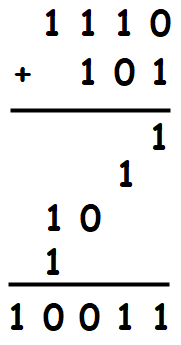
得到了`10011`这个结果,我们将三个二进制转化成十进制验证一下:`1110 = 14`,`101 = 5`,`10011 = 19`,完全正确。
当我们熟悉了二进制的计算过程后我们会发现,其实二进制的加法计算要比十进制更简单,因为二进制的最低位的计算只有三种:`1 + 0 = 1`、`0 + 0 = 0`、`1 + 1 = 10`,比十进制要少得多,毕竟二进制一共也只由`0`和`1`两种数字组成。
## 1.2 浮点数
上面说的例子是整数的运算,精通十进制计算的我们知道,在十进制的计算中,小数的加法和整数大同小异,依然是从最右边开始相加,往左边进位,直到整个数字的位数遍历相加完毕,譬如:`5.875 + 3.75 = 9.625`。十进制是如此,二进制也不例外,我们把上式中的前两个数字换成二进制:`5.875 = 101.111`,`3.75 = 11.11`,然后把这两个二进制浮点数相加:

注意,带小数的计算,我们需要将小数点对齐。经过计算,`101.111 + 11.11`得到的结果`1001.101`对应的十进制数正是`9.625`。
# 2 减法
讲完了加法,下面来看减法。众所周知,减法是加法的逆运算,并且减法的运算也依然是从最右边开始,逐渐往左。由于是加法的逆运算,我们需要注意的是,在减法中,没有进位,取而代之的是退位。我们直接来看上面加法部分的最后一个式子`101.111 + 11.11 = 1001.101`的减法逆运算:
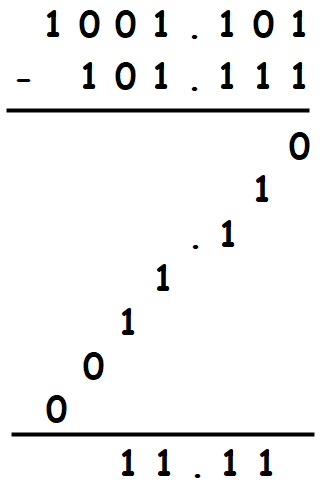
上面的竖式就是`1001.101 - 101.111`的过程了,**式中的每一步我都直接计算了退位**。这个式子比较特殊,它除了右边第一位外,一路往左全部都在做退位计算,所以整个竖式看起来有点诡异。但总之,我们得到了`11.11`这个结果,和上文中的加法吻合。
关于减法还有一点,就是减数>被减数的情况,我们知道,这种情况的结果为负数,而我们在计算的时候,其实只需要把不存在的位数都用`0`去替换,该怎么退位怎么退位就行了,这里就不再展开。
# 3 乘法
## 3.1 整数
从加减到乘除,我们的计算又提升了一个维度,而乘法实际上也是加法的进阶,所谓乘,其实就是倍数,也就是几个几相加,如`4 × 3`,实际上就是`4`个`3`或者`3`个`4`相加。
还是先来看十进制,取两个数:`84`,`57`,我们用竖式来看一下他们的运算过程:

嗯,看上去比加减法复杂多了。但仔细观察我们就会发现,每一行数字其实就是两个因数上各个数字遍历相乘的结果,唯一要注意的,就是相乘后所在的位置,我们逐行来看。
首先第一行,`4 × 7 = 28`,这个没有任何问题,`4`和`7`都是个位数,也就是\\(10^0\\)位置上的数,因此它们之间相乘,就是两个个位数相乘,结果的最低位在个位上。然后是第二行,这里的`56`是`7 × 8`的结果,但实际上,式中的`8`并不是`8`,而是`80`,是十位(\\(10^1\\))上的数字,因此它和个位上的`7`相乘,得到的应该是`560`,而我们在式中把`0`给省略了。或者换一种角度,`56`这个数字最低位所在的位数,实际上是`8`的位数和`7`的位数相乘的结果:\\(10^0\times10^1=10^1\\),因此`56`就被写到了\\(10^1\\)的位置上,如果把个位看作是第`0`位,那么`56`所在的十位就是第`1`位。
下面一行的`20`和上面`56`一样。
最后一行,`40`,经过前面的分析我们知道,它其实是`50`和`80`相乘的结果,后面两个`0`省略了。但为了下面二进制讲解时方便,我这里更愿意使用所在位数来解释,也就是\\(10^1\times10^1=10^2\\),也可以直接指数部分相加`1 + 1 = 2`,所以`40`就被写在了从`0`数起的第`2`位上。
最后把上面四行所得的数字按照位置相加,不存在的地方用`0`补充,就得到了最终结果`4788`。
再来看二进制,实际上二进制的乘法要比十进制省事儿得多,原因和加法一样,因为二进制只有`0`和`1`两个数,因此它的基础乘法计算只有三种:`0 × 0 = 0`,`0 × 1 = 0`,`1 × 1 = 1`,连进位都省了,全是一位。
我们取两个二进制整数`110(6)`和`101(5)`,来看看它们相乘后的结果:
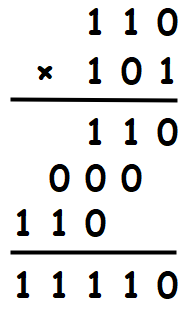
由于二进制的基础乘法实在太简单,我这里没有像上面十进制一样,遍历每个数字相乘,而是将第一个因数`110`看作一个整体,将第二个因数`101`的三个数拆开,分别去乘`110`,所以我们看第一行结果`110`,是`1 × 110 = 110`,由于`1`在第`0`位,所以结果也写在第`0`位。
接着是第二行,`0 × 110 = 000`。这个`0`在`101`的\\(2^1\\)所在的位置上,也就是第`1`位,而看做整体的`110`的最低位为\\(2^0\\),也就是第`0`位,因此他们相乘的积也写在第`0 + 1 = 0`位。
第三行,`1 × 110 = 110`。`1`在第`2`位,所以结果写在第`0 + 2 = 2`位。
最终把上面三个数相加,就得到了`11110`,也就是`30`,正好是`5 × 6`的结果。
## 3.2 浮点数
完成了整数的乘法后,我们来看小数带小数的乘法,鉴于二进制实在是太好算了,我们跳过十进制,直接来到二进制的例子。取两个数,`1.01(1.25)`,`11.1(3.5)`,来看他们的竖式计算:
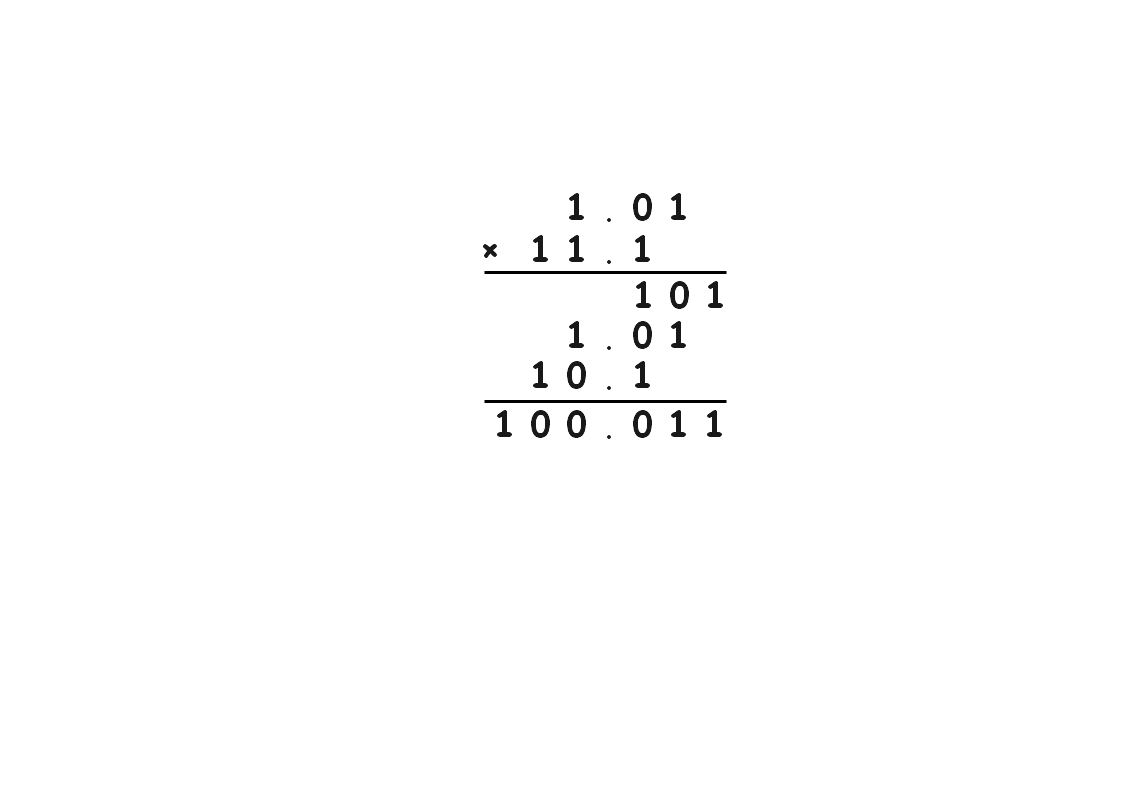
这里我们同样将第二个因数`11.1`拆开,将第一个因数`1.01`看做一个整体来计算,得到了最后的结果`100.011(4.375)`。这个浮点数相乘的式子里,我们同样要注意,并且特别注意位数的问题。
首先第一行,我们看到被我们看做整体的第一个因数`1.01`的最低位为\\(2^{-2}\\)位置上,即`-2`位,而与之相乘的`0.1`在`-1`位上,因此,第一行相乘的结果我们要写在第`-1 + -2 = -3`位上,所以它整个都在小数点后面。以此类推,第二行和第三行分别把结果最低位写在了`-2`和`-1`位上。最后把三个结果相加,不存在的位置用`0`补充,就得到了最终结果。
整体而言,二进制的乘法要比十进制的乘法简单的多得多,这回我们连九九乘法表都不用背了。
# 4 除法
除法是乘法的逆运算,但相对于加法的逆运算减法来说,除法就相对要复杂一些了。我们还是先从十进制开始,但这次就不区分整数和小数了,直接从浮点数开始。
取两个十进制数,被除数`185.65`,除数`2.5`,我们来计算\\(185.65\div2.5\\)的结果:
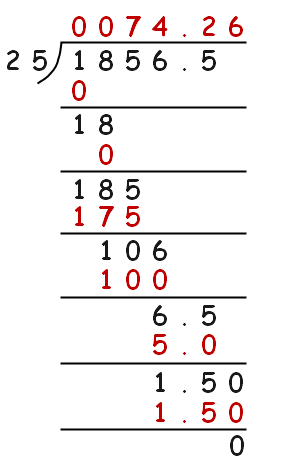
选的数字有点大,整个计算过程有点长。这里有几个点我们需要注意:
1. 在计算带小数的除法时,我们会习惯先将除数(`2.5`)变成整数,也就是除数和被除数同时乘\\(10^n\\),这里两个数在除之前都先乘了`10`:\\(185.65\times10\div(2.5\times10)\\),使`2.5`变成了`25`。这样做可以方便计算,原因就是前文乘法中我们强调过很多次的位数问题,因为在除法的过程中也涉及乘法,即`被除数=除数×商`,如果我们把除数的小数点去掉了,那么除数的最低位变成了第`0`位,我们在计算时就会方便很多,不用担心位数搞错的问题。
2. 除法在计算时,从最高位开始计算,以被除数为基准数,每一位上的数除以整个除数,若当前的数小于除数,则结果为`0`,并将当前计算的数减去`0`后与下一位相结合(作为下一位的高一位)成新的数字,再除以整个除数。如上式中第一步和第二步,结果都是`0`,然后把两步的结果与下一位结合,变成`185`,此时可以除以`25`,`25 × 7 = 175`,`185 - 175 = 10`,然后下一步将这个`10`和被除数的下一位`6`结合,得到了`106`。上式的计算过程部分中,所有商与除数相乘的结果都是红色字,新的每一步的被除数都是黑色字。这样一直计算,直到最后剩下的结果为`0`,我们就得到了最终的商,上式中写在被除数上方的`74.26`。
上面我文字写的有点绕,但其实只要我们大概回忆一下十进制的除法,通过上面这个式子,就能看明白是怎么回事了。
二进制同理,我们取两个二进制数`11.11(3.75)`,`10.1(2.5)`,来看一下\\(11.11\div10.1\\)的结果:

过程和上面十进制一样,最终我们得到了`1.1(1.5)`这个结果。
# 5 结尾
其实在原本的计划中,这篇(二)里还打算把二进制的位运算给放进来,这样凑成一个完整的`运算`篇。但吃了上一篇文章篇幅过长的教训后,觉得还是先不写运运算了,在下一篇专门来讲运运算,以节省篇幅,提升一点阅读体验。